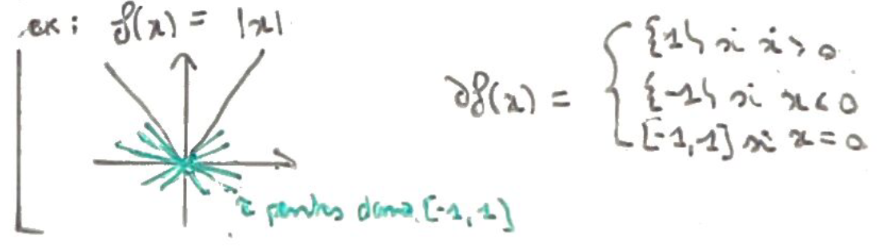Sous-différentielle \(\partial f(x)\)
Ensemble de directions possibles de pentes qui sont en-dessous de la fonction.$$\partial f(x):=\{h\in H\mid\forall y\in H, f(y)\gt f(x)+\langle{h,y-x}\rangle \}$$

• généralisation du concept de Différentielle aux fonctions non différentiables
    
• pour une fonction différentiable, \(\partial f(x)\) \(=\{\nabla f(x)\}\)
• on appelle \(h\in\partial f(x)\) un sous-gradient
    
• caractérisation : $$\forall y\in H,\quad\lim_{t\to0^+}\frac1t\Big( f(x+t(y-x))-f(x)\Big)\geqslant\langle{h,y-x}\rangle $$
• \(\partial f(x)\) est toujours un ensemble convexe
  Fermé (éventuellement vide)
• permet de caractériser les minimums \(x\) de \(f\) : \(0\in\partial f(x)\)

Questions de cours

START
Ω Basique (+inversé optionnel)
Recto: Quelle est la sous-différentielle de \(f(x)=\lvert x\rvert\).
Verso:

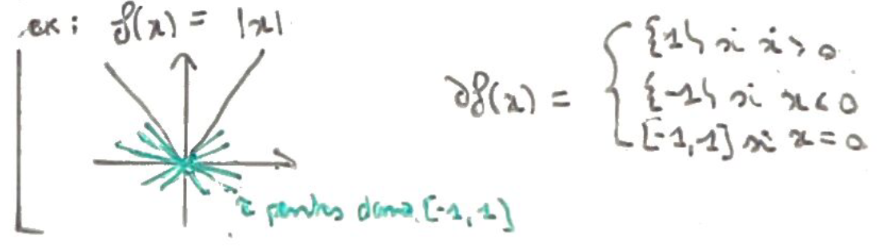
Bonus:
Carte inversée ?:
END

Démontrer \(2)\) :

L'inégalité \(\forall y\in H,f(y)\geqslant f(x)\) permet d'avoir la définition de \(0\in\partial f(x)\).

START
Ω Basique (+inversé optionnel)
Recto: Donner un exemple de fonction \(f\) pour laquelle \(\exists x\in\operatorname{dom}(f),\partial f(x)=\varnothing\).
Verso: $$f(x)=\begin{cases}+\infty&\text{si}\quad x\lt 0\\ -\sqrt x&\text{sinon.}&\end{cases}$$
Bonus:
Carte inversée ?:
END

Exercices

Développer la définition \(h\in\partial f(x)+\partial g(x)\) : il existe une décomposition \(h=h_f+h_g\), avec \(h_f\in\partial f(x),h_g\in\partial g(x)\).

Additionner les deux inégalités nous donne le résultat.